Tuesday, August 15, 2017

Day 29

---

Today we had our practice presentations in the auditorium with Joe and Matt. Everyone's presentations went pretty well although a few were too long (including mine which was about 1.5 min over the time limit). I think the amount of information and number of slides is reasonable but I need to practice a few more times today and tomorrow to help cut down on the time for my explanations of each slide. Final versions of our presentations are due tomorrow at the end of the day so I'll ask Dr. Qiao to look at my edited version one more time before submitting the final copy to Joe.

Monday, August 14, 2017

Day 28

---

Dr. Qiao came to the lab this afternoon to review our presentations for later this week and give is suggestions for what needed to be edited to be made clearer or more concise. Dr. Qiao also helped me to change the order of the presentation slightly to make it more cohesive. We didn't have time to actually practice presenting them to Dr. Qiao which we will still need to do before Thursday but our practice tomorrow should help to improve the presentation as well once we get feedback from the other interns and from Joe.

Friday, August 11, 2017

Day 27

---

This morning, Dr. Qiao helped Ronny and I prepare for our mini presentation for the Dean of the college of science. We each prepared three slides and practiced presenting to Dr. Qiao. Hopefully this practice will help to improve our presentations next week too.

When the Dean arrived at the lab Dr. Qiao showed her the femtosecond laser system which was new since the last time she visited. Then Lauren, Ronny, Cayla, and I talked to the Dean and answered a few questions about the work each of us is doing while we presented our slides. The Dean seemed to be impressed by the research the lab is doing and was interested to see how Ronny and I had been able to learn from and contribute to the ongoing work here.

Thursday, August 10, 2017

Day 26

---

Today I worked on creating a short presentation at the request of Dr. Qiao that will be presented to the Dr. Maggelakis, the Dean of the College of Science, who will be visiting our lab tomorrow. Everyone working in the lab will be making a giving a short presentation on their current project and what they have learned in the lab.

I also continued working with the delay box for a short time and realized that the minimum delay time between the two pulses was about 5 nanoseconds; the manual says that the range starts at 0 and has a resolution of 5 picoseconds so I'm not sure why it won't go below 5 nanoseconds.

Wednesday, August 9, 2017

Day 25

---

I was able to figure out how to operate the delay box that we want to use to trigger the CCD camera and laser despite a not very helpful manual. I set the pulse to trigger two pulses through two separate output cables that were 50 nanoseconds apart and each lasted for 5 nanoseconds. This will be used to trigger the camera after a very short delay so that the laser has time to reach sample before the camera begins its exposure. The delay box settings were tested used an oscilloscope which displays electrical input signals. Ronny is working now to find a way to connect the delay box to the camera because they do not use the same type of cable.

Delay box (right) connected to oscilloscope (left)

Tuesday, August 8, 2017

Day 24

---

I think the program I am working on is calculating the complex beam parameter (q) correctly now that I changed it to use the input beam waist location in the calculation of the radius of curvature rather than calculating that position based on the waist size and current size; I'm not sure why the second way doesn't work though, it seems like it should give the same answer either way.

The program calculates the q value and then uses q in a 1x2 matrix which is multiplied by the matrices for the components of the optical system (one matrix for each lens and one for each distance of free space between, before, or after lenses) which gives a new complex parameter. The same process can also be done to the two values (height and angle) that are used to calculate the radius of curvature. By knowing the radius of curvature before and after the transformation the beam radius and therefore intensity (because power is conserved) can be calculated at the second point as well because radius and radius of curvature are the only two variables used to calculate q (several constants are used as well). MATLAB is used for this process because instead of just calculating the new beam characteristics at the end point, it can run through a loop and find the beam characteristics at every point between two desired distances and display them as a data table or a graph.

Monday, August 7, 2017

Day 23

---

Today I worked on revising my outline and creating my presentation for a large part of the day so there isn't much exciting news to report. I worked on the MATLAB program later and I think the matrix transformation is not giving me the correct result (assuming my calculation on paper is correct) but I'm not sure what the problem is yet.

Friday, August 4, 2017

Day 22

---

Today was the research symposium for REU (Research Experience for Undergraduates) students who have been working on a research project at RIT over the summer. I attended 3 of the talks about research in astronomy and cosmology. One of the presentations was about the technical aspects of creating a cryogenically cooled imaging system for use in a telescope. Two of the presentations referred to analysis of large amounts of data from the COSMOS database which is a sky survey created by Caltech that I had not heard of previously. The survey records data of over 2 million galaxies in a small 2 square degree patch of the sky. The analysis of data in these two talks were very interesting. One focused on the star formation rate in galaxies and how it changed over the timespan of the universe and the other talked about the galaxy merger rate of large galaxies.

I think I'm close to finishing the portion of my MATLAB program that I've been working on this week as I calculated an ABCD matrix transform of a beam but I still need to check part of it by hand to make sure it is giving the correct result.

Thursday, August 3, 2017

Day 21

---

This morning Ronny and I met with Dr. Qiao after she arrived back from China yesterday. She wanted to check in on our progress and gave us some helpful tips on improvement of our outlines and presentations.

After meeting I continued to work on my MATLAB code for the rest of the day as I still haven't completed the function for transforming a Gaussian beam after in passes through an optical element. I first wanted to attempt to calculate an ABCD matrix transformation on paper to make sure I understood it completely (which I didn't at first) before trying to code a function to do the same thing.

Wednesday, August 2, 2017

Day 20

---

Today was Wednesday meaning there was a tech talk at noon today (the last one for the summer), which I attended. The talk was about a software system called DIRSIG that is able to simulate hyperspectral image data in many different regions of light to test imaging systems before they are deployed for use in remote sensing. The software is able to accurately simulate a variety of different scenes including cars, buildings, and geographical features in order to test the capabilities of systems for use on high altitude planes and satellites.

Later today I also assisted in Titus' research by acting as a test subject for him. I wore a set of eye-tracking glasses that recorded my eye movements and gaze position as I performed several activities. I first had to catch a tennis ball repeatedly that was bounced off the floor. I then had to walk around the second floor of the Carlson building and then be pushed on a cart in the same path around the second floor. Next we went to a different building at RIT to record my eye movements again as I took a path around the building (this time unguided) and then was pushed on a cart around the building. I won't say why each of these tests was necessary because it could bias anyone else who participates in the experiment to know the purpose and what Titus was looking for in the data beforehand. It was pretty fun to help with the experiment and hopefully I gave Titus some useful data for his project.

Tuesday, August 1, 2017

Day 19

---

I spent today trying to figure out why my program to model the Gaussian beam is showing diffraction even though I removed the aperture that it was originally programmed to propagate through. I didn't fully fix the problem but I did eventually identify one error (I forgot to square one of the variables in a function I was calling) that was causing the calculated radius to be incorrect.

Monday, July 31, 2017

Day 18

---

Dr. Qiao asked Ronny and I to start working on our presentations so that we have plenty of time to edit and refine them before August 17th. I spent a lot of time today working on that; it took a while to insert all of the equations I've been using as equations in PowerPoint.

Other than I working on my presentation I confirmed the calculations of my 3D Gaussian program in MATLAB with the results of the same calculation in 2 dimensions just to check that the program was working correctly. Below is an image of the phase of the beam in 3 dimensions that turned out to have a particularly interesting diffraction structure.

Outline

---

1. Summary

a. A femtosecond laser beam can be used for ablation based material removal and welding of different materials
b. A BPM was constructed to model the propagation of a laser beam and the interaction of the beam with different optical substrates

2. Uses of laser for material removal in optical finishing, welding for creation of photonics devices

a. High intensity of femtosecond laser can cause nonlinear optical effects which can be utilized for these purposes

3. Diagram and explanation of setup for experiment showing laser and sample (silicon)
4. Model of Gaussian (picture), radially symmetric

a. Beam propagates as a Gaussian, radius and intensity change over distance

5. Mathematical description of beam propagation, description of changing variables
6. MATLAB was used to create matrix representation of grid (spatial) where the intensity of the beam is calculated at each point, initially in air
7. Beam parameters are used in equation to create a simulation of beam propagation in different materials using MATLAB

a. Parameters include wavelength of light, focus distance, and minimum beam size
b. Matrix is used to transform beam parameters when laser passes through a lens or optical substrate

8. MATLAB can also be used to model nonlinear effects such as self-focusing which can be used in welding of materials
9. Summary of results of simulations
10. Experimental data collected and comparison to simulation (if completed before end of internship?)
11. Conclusion: restate summary

Friday, July 28, 2017

Day 17

---

Ronny and I continued experimenting with our "camera" system today using the CCD along with a 20x magnification microscope objective. We were able able to produce a sharp image showing the fine detail of the fiber light we had used previously.

We also experimented with different shutter speeds on the camera to determine if we could capture an image of a momentary phenomenon (flicking the light on and off) by leaving the CCD shutter open for several seconds during which time the light would blink for less than a second. We were successful in doing so, however, the image produced had much less resolution than previous images using a shorter exposure time with a constant image source. It will most likely be necessary to use a similar technique to capture an image of the femtosecond laser beam due to the extreme difficulty of triggering the CCD shutter to coincide perfectly with the arrival of a laser pulse moving at 299,792,458 m/s with a duration of 10^-15 seconds; simply leaving the shutter open long to enough to ensure arrival of the pulse within a certain time range would be an easier way to capture the necessary image.

Thursday, July 27, 2017

Day 16

---

I started work today around 12:30 as we have a field trip later to the Mees Observatory that will be counted toward our hours for the day and therefore we did not need to come in for a full day of work in addition to a 4 hour field trip. Ronny and I continued experimenting with several convex lenses today in order to produce an image that could be captured with our CCD camera using a script Ronny wrote in MATLAB. We were able to produce an image of Ronny's phone (the object needed to be backlit and we didn't have anything transparent so an electronic screen worked well) with enough resolution to distinguish individual pixels. The lens we will be using for the laser experiment will be a microscope objective so that we can see much finer detail on the silicon sample after it is ablated by the femtosecond laser.

Dmitry (who recently got his PhD from RIT) organized the field trip and I was asked to help as I am one of the regular tour guides at the Mees Observatory during the summer. We left around six for our field trip and stopped at Amiel's Sub Shop for dinner. The bus we took had fabric cushioned seats and overhead storage (a lot nicer than school buses). We got to the observatory site around 8 and drove up the hill to the Gannett House where normal tours start with a presentation. I gave the presentation while Adam (another guide who is a student at U of R) set up the telescope. Once it was beginning to get dark, we walked up the hill to the observatory building. Dmitry and I showed the other interns the control room downstairs. By the time it was dark enough to start observing the sky was completely cloudy. Hopefully it was still interesting for everyone to learn about the telescope and observatory even though we didn't get to do any astronomy.

Wednesday, July 26, 2017

Day 15

---

Ronny and I worked today on calculating the correct distance to place the CCD camera within the setup for the femtosecond laser. We initially investigated image formation in a camera as the system used to form an image of the silicon surface on the CCD is very similar to the way a lens transforms light to form an image on the sensor of a DSLR. We were able to determine that a system of equations that both incorporated the distance from the object to the lens and the distance form the lens to the image (CCD) could be solved by inputting the desired size of the image (size of the CCD sensor) and the known size of the object being imaged. I was able to write a simple program in MATLAB utilizing its ability to solve systems equations in order to automate the process of determining these distances. We later constructed a basic system using a fiber light and a convex lens to verify our calculations of the distance from the lens to the image plane.

Although it is difficult to see in the image above, when the paper is placed at the correct distance from the lens, the light resolves to form an image of the interior glass structure of the fiber light.

Tomorrow I may be assisting Titus in data collection for his project by participating in an eye-tracking experiment. He originally planned the experiment for today but due to technical difficulties with the glasses used to record motion of the eye it was postponed; hopefully he is able to repair them as I'm excited to help out with his project.

Tuesday, July 25, 2017

Day 14

---

I turned in my permission slip this morning for the field trip to Mees Observatory later this week. I will be helping with the field trip as I have been a tour guide at the observatory for 3 years as a member of the Rochester astronomy club, ASRAS. Unfortunately the forecast for Thursday looks like it will be mostly cloudy so we may not get to do much observing through the telescope while we are there; however, the view from the back patio of the Gannett House is impressive in any weather so there's always that to look forward to.

Today I worked on writing the outline for my presentation, with some suggestions from Lauren, and continued integrating a transformation matrix into my BPM program in MATLAB.

Monday, July 24, 2017

Day 13

---

Today we had a visitor who was taking pictures for an article about the program to be given to Monroe County educators. She took pictures of Ronny and I pretending to do something with the laser (Lauren wasn't there so we couldn't actually use the laser but she wanted an exciting picture).

I continued my work on creating a BPM for the Gaussian beam we will be modeling by incorporating a matrix that can be used to transform the beam as it passes through an optical element (lens, mirror, etc.) or moves into a material with a different index of refraction.

Friday, July 21, 2017

Day 12

---

Today was Friday meaning the grill was set up outside the building for the weekly cook-out. I think all of the interns were outside today for lunch even though not everyone brought food to grill. I brought pizza to warm up on the grill and I ate outside which was a nice break from sitting in a windowless basement laboratory all day.

I continued working on my project from yesterday which was to adapt a BPM to simulate a Gaussian beam rather than a circular beam traveling through an aperture. The code I wrote models the intensity and phase of the beam from 50 cm before to 50 cm after the focal point. The radius of the beam is given by the function w(z), where z is the distance along the axis of propagation, and is shown below the intensity plot on the diagrams below. The smallest possible radius occurs at the focus and for this beam it is 0.1 cm.

Thursday, July 21, 2017

Day 11

---

Today I worked mostly on translating a program written in Python into MATLAB which was pretty easy as Python and MATLAB are very similar in that they are both dynamically typed languages and have nearly the sane library of functions even though some are called differently. However, the developers of MATLAB have, for no apparent reason, decided that the first index of an array should be 1 instead of 0 like it is in almost every major programming language.

This program was originally written by Lauren to model the diffraction of light as it passed through an arbitrary aperture. I will be adapting it to model a Gaussian beam propagating through air.

Wednesday, July 19, 2017

Day 10

---

Today I continued to work on programming a standard BPM for a laser traveling through air. The model I created yesterday predicted the radius of the beam as it comes to a focus; this model shows the intensity of the beam (vertical axis) as it passes through the same focal point. Because power is always conserved, the intenisty of the beam increases as the radius decreases.

Tuesday, July 18, 2017

Day 9

---

At our meeting this morning we read through the first few abstracts to begin giving each other feedback and advice on improvements that could be made. From what we went over this morning, I decided to edit my abstract somewhat today in order to make it more understandable and remove some unnecessary background information while adding more information about certain terms.

Today I worked largely on modeling a standard beam as it would travel through air using MATLAB to plot functions of intensity and beam radius over time. The image below is a model of the radius of a beam as it passes through its focus point after being focused by a lens:

Monday, July 17, 2017

Day 8

---

Joe was back at our morning meeting today and he reminded all of us to have our abstracts posted on our blogs by tomorrow morning so that we can peer-reveiw each other's and offer suggestions.

In the lab today I continued work on the program I have been analyzing which will be used to simulate the interaction of a laser beam with glass, silicon, and other optical substrates. This program will model a beam propagation method which simulates the intensity distribution of the laser as it passes through materials.

Abstract

---

A high-intensity, femtosecond laser beam propagates through a medium in such a way that nonlinear effects are observed. A simulation method is desired to model the intensity distribution of a focusing beam as it interacts with the surface and within the bulk of an optical substrate; such an interaction would enable both the creation of photonics devices by welding through glass and optical finishing by removal of material through ablation. A beam propagation method will be constructed to simulate the intensity distribution of a beam as it is travels initially through air and is then altered by the nonlinear effect of self-focusing, a process in which the beam can travel through a flat substrate as opposed to a curved lens and still become focused with the substrate as the material is altered by the high intensity of the beam.

Friday, July 14, 2017

Day 7

---

After our meeting this morning, I spent a lot of time analyzing some MATLAB code I'll be using and adding to for my project. Fortunately the online list of MATLAB libraries is more readable than the one for Java and even includes tips for using functions in certain situations.

Later today, Lauren arrived at the lab on her flight back from the conference in Denver (which was supposed to be at 10:30 but got delayed for 6 hours) and we discussed in greater detail the project I will be working on and she gave me a few helpful comments on my abstract.

Thursday, July 13, 2017

Day 6

---

This morning Matt showed us a video about the freshmen imaging science class at RIT. The class is very unique as it does not have any "normal" teaching through lectures and homework but instead consists of a year long project that everyone in the class works on together. Students teach themselves what they need to know in order to complete the project. Their project is then featured at the Imagine RIT festival at the end of the year. Although I do not intend to major in Imaging Science this class is a unique idea and I agree with Titus' comment during our meeting that this type of learning can and most likely should be implemented in other courses as well.

Cayla and Dr. Han were not in the lab today so most of today was spent working on my abstract and reading through scientific papers relevant to my project for the summer.

Wednesday, July 12, 2017

Day 5

---

Today at our morning meeting Matt was able to show us the video he planned to yesterday which was a brief overview of the different applications of imaging science and emphasized the diversity of research fields it is used in.

After working on my abstract in the morning I assisted Cayla with the alignment of mirrors and lenses on the optics table. This process involves perfectly aligning a series of mirrors, lenses, beam splitters, and sensors individually by hand; it took up until lunch time and then had to be continued for some time afterwards as well. After finishing I studied optical (dielectric) waveguides and Beam Propagation Methods for the rest of the day as they are very relevant to my project which will attempt to simulate the intensity distribution of a short pulse laser beam when it interacts with a glass object or surface so that a laser can be used for fabrication of glass elements for photonics.

Tuesday, July 11, 2017

Day 4

---

Our meeting was pretty short this morning; Joe is out this week so Matt Casella will be running our daily meetings. He had planned to show us a video about Imaging Science but a lack of computer speakers postponed that until tomorrow's meeting.

Today I expanded the previous day's learning of Fourier series with Fourier Transforms, a way of processing a waveform in the time domain (an amplitude vs. time plot) into the frequency domain (an amplitude vs. frequency plot). As I discussed in my previous post, any continuous waveform can be broken down into a series of sine and cosine waves; a frequency domain plot shows each frequency present in a more complex waveform compared to the amplitude of that frequency essentially showing "how much" of each frequency is present in the overall waveform. For example if we take a waveform with a known equation such as the graph of:

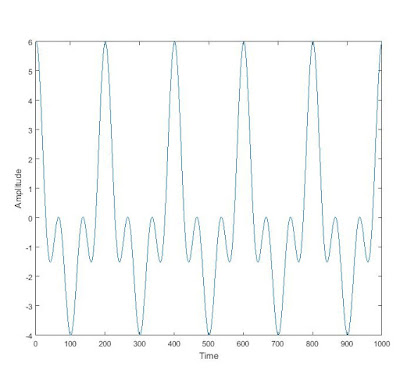
We know the frequencies of the components of this graph to be 10, 20, and 30 but a waveform obtained from experimental measurement would not be a perfect periodic cycle and we would not know the equation. A Fourier transform, however, can plot a data set in the frequency domain rather than the time domain and we can thereby determine the most prevalent constituent frequencies and their relative amplitudes:

A more complex waveform would most likely contain a wide spectrum of frequencies rather than a small number of discrete frequencies but many would have an amplitude close to zero and appear similar to "background noise" on the frequency domain plot.

Monday, July 10, 2017

Day 3

---

This morning Joe introduced us to Matt Casella; he will be running our daily meetings while Joe is out this week. We received an informational page detailing what should be contained in our abstracts (which must be completed by Monday). I have not yet begun work on my project because Lauren (the grad student I will be working with on the project) is still away at a conference with Dr. Qiao so I'm hoping to get enough detail on the project this week to be able to write an effective abstract.

Working in the lab today, I learned about Fourier Series, a method of breaking down any continuous waveform into an infinite series of only sine and cosine waves of different amplitudes and frequencies. For example a square wave with a period of Π appears like this on an amplitude vs. time plot:

But a Fourier Series can create an equation that will more accurately approximate the shape of the graph as you add more terms to the series and an infinite number of terms would exactly equal the square wave.

The way the coefficients are calculated was new to me (mostly a lot of Trig integration identities) but the concept is very similar to a Taylor or MacLaurin series in calculus.

Friday, July 7, 2017

Day 2

---

We started today with a short meeting with the other interns and Joe in our usual meeting room upstairs. Joe gave us a calendar of our major deadlines and special events for the rest of the summer. I'm excited to go see one of the Wednesday presentations; they sound like fun (plus there's free pizza and popcorn).

After finishing our meeting upstairs Ronny and I went down to the lab to get started on our work for today. Cayla brought in some textbooks for us to look at to start learning the basics of optics and quantum physics. It took me at least half and hour to get through the first page of the chapter on the Schrodinger equation but after that the rest of the chapter was pretty smooth, mostly just conceptual with some integrals that are used to determine the probability of finding a particle in any given region of space. Aside from that we worked on some more MatLab and started looking at some of the programs we will be using to process data once we start working on experiments with the laser.

Thursday, July 6, 2017

Day 1

---

We started out first day of the internship with a meeting where we got to know the names of all the other interns at RIT this summer. We all introduced ourselves and told each other an interesting fact or favorite activity of ours. After Joe finished going over some basic rules (don’t steal stuff from RIT, etc.) we went down to the Red Barn to participate in some team building exercises with a man named Tom. Tom lead us in group activities and helped us develop more creative ways of thinking about and working together to solve problems.

After arriving back at the Carlson building and having lunch, the interns split up and each met with their respective advisors. Ronny and I already met with Dr. Qiao earlier this week because she is currently traveling to a conference with one of her grad students. After arriving at the lab today and meeting with Cayla and John, two of the other grad students working there, Ronny and I took an online laser safety training course online. The government and RIT require anyone working with a Class 4 laser to take a safety course before use.

Once we finished this training and received our certificate we began learning MatLab, a program commonly used to process and plot data collected in series of experiments. I didn’t think it was too difficult to learn the syntax of the MatLab programming language because I have taken courses in Java in school and learned some C++ independently. The only thing that was unusual about the language is that the data types of variables are not defined and can be changed as operations are performed on them; it took a while to get used to that because Java and C++ both require you to define data types as variables are declared and mismatched data types will give you a syntax error and stop your program from running.

Overall I enjoyed the first day of our internship and look forward to the next six weeks!